La page web de Monsieur Adam

Histoire de rectangles : le format A4

Vous êtes ici : Accueil du site > Culture > Histoire de rectangles : le format A4

Par : Monsieur Adam
Publié : 16 mai 2009
Modifié : 4 août 2009
Version imprimable (PDF)

Chapitre 1 : rectangles de même forme (niveau 6e-5e)

Observons ces deux rectangles :

Ils n’ont pas la même forme : le premier est gras, le second est maigre.

Que dire de ces deux-ci ?

Ils n’ont pas la même taille, mais ils ont quelque chose en commun : ils sont tous les deux construits par assemblage de deux carrés. Autrement dit, leur longueur est le double de leur largeur. Il semble alors raisonnable de dire que ces deux rectangles "ont la même forme".

Plus généralement, dans quel cas dirons-nous que deux rectangles ont la même forme ? nous avons dit des deux rectangles précédents : "leur longueur est le double de leur largeur". Et si nous remplacions "double" par "triple" ?

Nous obtenons encore deux rectangles "de même forme", bien sûr. Et nous pourrions aisément continuer en remplaçant "triple" par "quadruple", "quintuple", etc.

Traduisons en mathématiques la phrase "La longueur du rectangle est le double de sa largeur" :

$Longueur=2\times largeur$

Si l’on remplace "double" par "triple", il suffira de remplacer 2 par 3 :

$Longueur=3\times largeur$

Pour comparer les formes de deux rectangles, il pourra alors être intéressant de se demander pour chacun d’entre eux : "par quel nombre faut-il multiplier la largeur pour trouver la longueur ?".

Ce nombre n’est autre que le quotient (ou rapport) : $\frac{Longueur}{largeur}$

Un dernier exemple : que dire des deux rectangles suivants ?

Nous avons très envie de dire qu’ils ont la même forme, puisque le second est obtenu en doublant les dimensions du premier : c’est un simple agrandissement, comme pourrait le faire une photocopieuse.

Pourtant, le rapport $\frac{Longueur}{largeur}$ n’est pas un nombre entier cette fois : c’est une fraction, et même une fraction assez désagréable : $\frac{35}{22}$ pour le premier rectangle, $\frac{70}{44}$ pour le second.

Mais souvenez-vous : la fraction $\frac{1}{3}$ peut encore s’écrire $\frac{2}{6}$ ou $\frac{3}{9}$ . Plus généralement, on obtient une fraction égale si l’on multiplie numérateur et dénominateur par un même nombre entier.

Ainsi, $\frac{35}{22}=\frac{35\times2}{22\times2}=\frac{70}{44}$ , et le rapport $\frac{Longueur}{largeur}$ est le même pour les deux rectangles !

Conclusion : on dira que deux rectangles ont la même forme s’ils ont le même rapport
$\frac{Longueur}{largeur}$

Ce rapport sera appelé la proportion du rectangle.

Par exemple, le rectangle suivant : a pour proportion 5.

Chapitre 2 : rectangles magiques (niveau 6e-5e)

Plions un rectangle en deux dans le sens de sa longueur :

Le petit rectangle obtenu a-t-il la même forme que le grand rectangle de départ ?

Pour le savoir, calculons les proportions de ces rectangles :

Pour le grand :

$p=\frac{9}{3}=3$

Pour le petit :

$p'=\frac{4,5}{3}=1,5$

Le petit rectangle n’a donc pas la même forme que le grand.

Faisons le même pliage sur un autre rectangle :

et calculons les proportions :

Pour le grand :

$p=\frac{10}{8}=1,25$

Pour le petit :

$p'=\frac{8}{5}=1,6$

Encore une fois, les proportions ne sont pas les mêmes. Elles semblent toutefois moins éloignées que dans l’exemple précedent… cela nous donne un espoir : celui de trouver un jour un rectangle "magique", qui ne changerait pas de proportion lorsqu’on le plie en deux !

Définition : on appellera (dans cet article) rectangle "magique" un rectangle qui, plié en deux dans sa longueur, ne change pas de proportion

En cherchant un peu à tâtons, on peut trouver le rectangle suivant :

Proportion du grand rectangle :

$p=\frac{7}{5}=1,4$

Proportion du petit rectangle :

$p'=\frac{5}{3,5} \approx 1,43$

Ce rectangle n’est pas magique, mais il n’en est pas loin !

En fait, il y a un rectangle que nous connaissons très bien et qui ressemble encore plus à un rectangle magique : c’est notre feuille de papier format A4 ! Ses dimensions sont $21 cm\times 29,7 cm$ . Sa proportion est donc $\frac{29,7}{21}\approx 1,4143$ . Si nous plions notre feuille en deux dans sa longueur, ses dimensions deviennent $14,85cm\times 21 cm$ et sa proportion $\frac{21}{14,85}\approx 1,4141$ . C’est presque magique !

Chapitre 3 : la proportion magique (niveau 4e-3e)

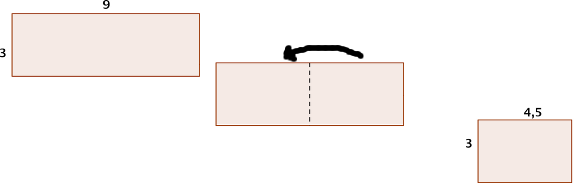
Revenons sur un exemple de pliage :

Les proportions sont : 3 pour le grand et 1,5 pour le petit.

Remarquons que la proportion a été divisée par deux. En effet, la longueur du rectangle a été divisée par deux, ou encore multipliée par $\frac{1}{2}$ , et la proportion $\frac{Longueur}{largeur}$ est devenue :

$\frac{\frac{1}{2}\times{Longueur}}{largeur}=\frac{1}{2}\times\frac{Longueur}{largeur}$

Cela se produit-il toujours ? La proportion est-elle toujours divisée par deux dans le pliage ? Non, comme le montre cet exemple déjà étudié :

Proportion du grand rectangle : 1,25. Proportion du petit : 1,6.

Quelle est donc la différence avec le cas précédent ? Observons que cette fois-ci la longueur du petit rectangle n’est plus la moitié de la longueur du grand, mais elle est égale à la largeur du grand !

Dans quelle situation cela se produit-il ? Chaque fois que la moitié de la longueur du grand rectangle est plus petite que sa largeur, autrement dit chaque fois que la longueur est moins que deux fois plus grande que la largeur, ou encore lorsque la proportion du rectangle est plus petite que 2.

Lorsque la proportion du rectangle est plus grande que 2, comme dans le premier cas, celle-ci est divisée par 2 dans le pliage, et le rectangle n’a donc aucune chance d’être magique.

Mais que devient la proportion dans le deuxième cas, si elle n’est pas divisée par 2 ? La longueur du petit rectangle est la largeur du grand, et sa largeur est la moitié de la longueur du grand. La proportion devient donc :

$\frac{largeur}{\frac{1}{2}\times Longueur}=\frac{1}{\frac{1}{2}}\times\frac{largeur}{Longueur}=2\times\frac{largeur}{Longueur}$

C’est à dire le double de l’inverse de la proportion initiale : si la proportion du grand rectangle est notée p, la proportion du petit est $2\times\frac{1}{p}$ ou encore $\frac{2}{p}$ .

Le rectangle est donc magique si sa proportion est égale au double de son inverse. En notant p cette proportion, l’égalité suivante doit être satisfaite :

$p=\frac{2}{p}$

Cette égalité n’est autre qu’une équation d’inconnue p.

multiplions par p les deux membres :

$p\times p=\frac{2}{p}\times p$

$p^2=2$

Et comme la proportion d’un rectangle doit être un nombre positif, il y a une seule solution à notre problème : $\sqrt{2}$

Conclusion : les rectangles magiques sont les rectangles de proportion $\sqrt{2}$

Chapitre 4 : le format A4 (niveau 3e)

En vérité, le papier format A4 est bien un rectangle magique. Si les proportions calculées plus haut ne sont pas exactement égales, c’est que les dimensions du papier A4 ne sont pas exactement $21 cm\times 29,7 cm$ .

Comment le format A4 a-t-il été conçu ? Il fait partie de la famille des formats A0, A1, A2 etc. qui ont tous la même proportion magique $\sqrt{2}$ et qu’on a définis de la façon suivante :

le format A0 est un rectangle magique qui a pour aire 1 m²,

le format A1 est obtenu en partageant le format A0 en deux dans sa longueur,

le format A2 est obtenu en partageant le format A1 en deux dans sa longueur,

etc.

Quelles sont les dimensions du format A0 ?

Si j’appelle x la largeur de ce rectangle, sa longueur est $x\times\sqrt{2}$ , et son aire est $x\times(x\times\sqrt{2})$ c’est à dire $x^2\times\sqrt{2}$ . Et comme cette aire vaut 1m², je peux écrire l’égalité :

$x^2\times\sqrt{2}=1$

Cette égalité n’est autre qu’une équation, que je sais résoudre :

$x^2=\frac{1}{\sqrt{2}}$

Cette équation possède une seule solution positive : le nombre $\sqrt{\frac{1}{\sqrt{2}}$ ou encore $\frac{1}{\sqrt{\sqrt{2}}}$ . C’est la largeur du rectangle A0. Sa longueur est $\sqrt{2}$ fois plus grande : elle vaut $\sqrt{2}\times\sqrt{\frac{1}{\sqrt{2}}$ .

Pour les spécialistes des calculs avec des racines carrées, simplifions un petit peu l’expression de cette longueur :

$\sqrt{2}\times\sqrt{\frac{1}{\sqrt{2}}}=\sqrt{2\times\frac{1}{\sqrt{2}}}=\sqrt{\sqrt{2}\times\sqrt{2}\times\frac{1}{\sqrt{2}}}=\sqrt{\sqrt{2}}$

Et l’on constate au passage que largeur et longueur sont inverses l’une de l’autre, ce qui n’est pas étonnant puisque leur produit est l’aire du rectangle, qui vaut 1.

Voici donc les dimensions du format A0 :

largeur : $\sqrt{\frac{1}{\sqrt{2}}}\approx0,841m$

longueur : $\sqrt{\sqrt{2}}\approx1,189m$

Pour les formats A1, A2, etc., on fait des divisions par deux. Voici les valeurs exactes et approchées de leurs dimensions en centimètres :

Format	Largeur (en m)	approx. (en cm)	Longueur (en m)	approx. (en cm)
A0	$\frac{1}{\sqrt{\sqrt{2}}}$	84,1cm	$\sqrt{\sqrt{2}}$	118,9cm
A1	$\frac{\sqrt{\sqrt{2}}}{2}$	59,5cm	$\frac{1}{\sqrt{\sqrt{2}}}$	84,1cm
A2	$\frac{1}{2}\times\frac{1}{\sqrt{\sqrt{2}}}$	42,0cm	$\frac{\sqrt{\sqrt{2}}}{2}$	59,5cm
A3	$\frac{\sqrt{\sqrt{2}}}{4}$	29,7cm	$\frac{1}{2}\times\frac{1}{\sqrt{\sqrt{2}}}$	42,0cm
A4	$\frac{1}{4}\times\frac{1}{\sqrt{\sqrt{2}}}$	21,0cm	$\frac{\sqrt{\sqrt{2}}}{4}$	29,7cm